A bináris keresés az egyik legegyszerűbb módja annak, hogy elemet találjon egy tömbben

Gyakran, a programozók, még a kezdők is,hogy vannak olyan számok, amelyekben meg kell találni egy bizonyos számot. Ezt a gyűjteményt tömbnek hívják. És megtalálni a megfelelő elemet, sokféleképpen lehet. De a legegyszerűbb köztük jobbra bináris keresésnek tekinthető. Mi a módszer? És hogyan lehet bináris keresést végrehajtani? A Pascal a legegyszerűbb eszköz egy ilyen program megszervezéséhez, ezért tanulni fogjuk.

Először is elemezzük, hogy mi a módszer előnyei, végül is, így megérthetjük,

mi a lényeg ebben a témában. Tehát, feltételezzük, hogy létezik olyan tömb, amelynek mérete legalább 100000000 elem, melyben meg kell találnia a konkrétat. Természetesen ez a probléma könnyen megoldható egy egyszerű lineáris kereséssel, amelyben a ciklust a kívánt elem és a tömbben létező elemek összehasonlítására használjuk. A probléma az, hogy az ötlet végrehajtása túl sokáig tart. Egy egyszerű Pascal programban többféle eljáráshoz és a fő szöveg három sorához nem fogod észrevenni, de ha több vagy kevesebb nagy projektet indítasz el sok elágazással és jó funkcionalitással, akkor a kész program túl hosszú ideig lesz betöltve. Különösen abban az esetben, ha a számítógép gyenge teljesítményt mutat. Ezért létezik bináris keresés, amely legalább kétszer csökkenti a keresési időt.

Tehát mi ennek a működési elvemódszer? Érdemes megemlíteni, hogy a bináris keresés nem működik semmilyen tömbben, hanem csak egy rendezett számsorban. Minden egyes következő lépésnél a tömb középső elemét (az elemszámra hivatkozva) veszi. Ha a kívánt szám nagyobb az átlagnál, akkor mindent, ami a bal oldalon van, vagyis az átlag elemnél kisebb, eldobható és nem kereshető ott. Ezzel ellentétben, ha az átlag alatti, a jobb oldali számok között nem keresheti őket. Ezután kiválaszunk egy új keresési területet, ahol az egész tömb középső eleme lesz az első elem, az utolsó pedig az utolsó lesz. Az új terület átlagos száma az egész szegmens ¼-e lesz, azaz (az utolsó elem + az egész tömb átlagos eleme) / 2. Ismét ugyanazt a műveletet végezzük el - összehasonlítjuk a tömb átlagos számával. Ha a kívánt érték kisebb, mint az átlag, dobja el a jobb oldalt, és addig addig végezze el, amíg meg nem találja ezt a középső elemet.

Természetesen a legjobb, ha megnézzük a bináris keresés megírásának példáját. A Pascal itt bárki számára alkalmas - a verzió nem fontos. Írjunk egy egyszerű programot.

Ez egy tömb lesz 1-től h-igA "massiv", az alsó keresési határt jelző változó, a "niz", a "verh" nevű felső határ, a keresés középső eleme "sredn"; és a szükséges szám "isk".

Tehát először adja meg a keresési intervallum felső és alsó határait:

niz: = 1;
verh: = h + 1;

Aztán megszervezzük a ciklust ", míg az alsó kisebb, mint a felső határ":

Míg niz <verh - 1 nem
kezdődik

Minden lépésben oszd meg a szegmenst 2:

sredn: = (niz + verh) div 2; {használja a div függvényt, mert megosztjuk a maradékot}

Minden alkalommal, amikor ellenőrzünk. Ha az átlag egyenlő a kívánt értékkel, megszakítjuk a ciklust, mivel a kívánt elem már megtalálható:

ha sredn = isk akkor megszakad;

Ha a tömb átlagos eleme nagyobb, mint amit keresünk, dobjuk el a bal oldalt, vagyis a középső elemet hozzárendeljük a felső határhoz:

ha massiv [sredn]> isk akkor verh: = sredn;

És ha éppen ellenkezőleg, akkor az alsó határt teszik:

egyéb niz: = sredn;
végén;

Ez minden, ami a programban lesz.

Elemezzük, hogy a bináris módszer hogyan fog kinézni a gyakorlatban. Vegyünk egy ilyen tömböt: 1, 3, 5, 7, 10, 12, 18, és keresd meg a 12-es számot.

Összesen 7 elem van, így az átlag a negyedik, értéke 7.

Mivel a 12 nagyobb, mint 7, az 1,3 és 5 elemek eldobhatók. Ezután 4 szám maradt, 4/2 maradék nélkül 2. Tehát az új középső elem 10 lesz.

Mivel 12 több mint 10, eldobja 7. Csak 10, 12 és 18 maradt.

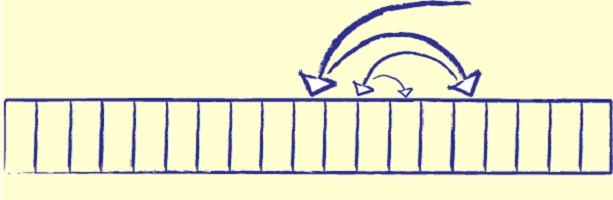
Itt a középső elem már 12, ez a szükséges szám. A feladat befejeződött - a 12-es szám megtalálható.