Hogyan keressük meg a kör sugarát: segítsük a tanulókat
Hogyan keressük a kör sugarát? Ez a kérdés mindig releváns az iskolás gyermekek számára, akik tanulmányozzák a planimetriát. Az alábbiakban több példát fogunk megvizsgálni, hogyan lehet megbirkózni a feladattal.
A probléma állapotától függően megtalálhatja a kör sugarait.
1. képlet: R = A / 2π, ahol A a kör hossza, és π egy állandó, egyenlő 3,141 ...
Formula 2: R = √ (S / π), ahol S a kör területe.
3. képlet: R = D / 2, ahol D a kör átmérője, azaz a szegmens hossza, amely az ábrán a középponton áthaladva két olyan pontot köti össze, amelyek egymástól annyira távol vannak egymástól.
A körkörös kör sugara
Először is, definiáljuk a kifejezést. A kört úgynevezett le, amikor megérinti az adott sokszög csúcsait. Meg kell jegyeznünk, hogy csak egy olyan sokszög körül lehet leírni egy kört, amelynek oldala és szöge egyenlő egymással, vagyis egy egyenlő oldalú háromszög, egy négyzet, egy rendes rombusz és így tovább. A probléma megoldásához meg kell találni a sokszög kerületét, és meg kell mérni annak oldalát és területét. Ezért vigye magával egy vonalzót, egy iránytűt, egy számológépet és egy tollal rendelkező noteszgépet.
A kör sugarának megkeresése, ha egy háromszög körül van írva
Formula 1: R = (A * B * B) / 4S, ahol A, B, B - a háromszög oldalainak hossza és S - a területe.
2. képlet: R = A / sin a, ahol A az ábra egyik oldalának hossza, és sin a a szomszédos szinusz számított értéke ennek az oldalnak a szemben.
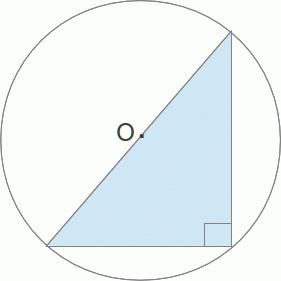
A kör sugara, amelyet egy jobb háromszög körül ír le.
Formula 1: R = B / 2, ahol B a hypotenuse.
Formula 2: R = M * B, ahol B - átfogója, és M - a medián lefolytatott hozzá.
A kör sugarának megkeresése, ha egy szabályos sokszög köré íródik le
Képlet: R = A / (2 * sin (360 / (2 * n))), ahol A az ábra egyik oldalának hossza, és n az adott geometriai alakban lévő oldalak száma.
Hogyan lehet megkeresni egy beírt kör sugarait?
Egy beírt kör akkor szólal meg, amikor a poligon minden oldalát megérinti. Nézzünk néhány példát.
Formula 1: R = S / (P / 2), ahol - S és P - az ábra területe és kerülete.
Formula 2: R = (P / 2 - A) * tg (a / 2), ahol P - kerülete A - hossza az egyik fél, és - szemben ezen az oldalán a szög.
A kör sugarának megkeresése, ha egy jobb háromszögbe van írva
1. képlet:
A kör sugara, amely a rhombusban van feltüntetve
A kört bármely rombuszban fel lehet tüntetni, mind egyenlő, mind nem egyenlő oldalú.
Formula 1: R = 2 * H, ahol H a geometriai alakzat magassága.
2. képlet: R = S / (A * 2), ahol S a gyémánt területe és A a hossza.
3. képlet: R = √ ((S * sin A) / 4), ahol S a gyémánt terület, és a bűn A az adott geometriai alak akut szögének szinája.
4. képlet: R = B * Г / (√ (² + ²), ahol В és Г a geometriai alak átlóinak hossza.
Formula 5: R = B * sin (A / 2), ahol B a rombusz átlója, és A a szög az átlós csúcsoknál.
A háromszögbe írt kör sugara
Ha a probléma állapotában az ábra minden oldalának hosszát adjuk meg, akkor először számold ki a háromszög (P) kerületét, majd az sempermérőt (n):
P = A + B + B, ahol A, B, B a geometriai alak oldalainak hossza.
n = n / 2.
1. képlet: R = √ ((n-A) * (n-B) * (n-B) / n).
És ha tudjuk, minden ugyanaz a három fél, akkor kapnak több és területe a szám, akkor lehet számolni a kívánt tartomány az alábbiak szerint.
2. képlet: R = S * 2 (A + B + B)
3. képlet: R = S / n = S / (A + B + B) / 2), ahol - n a geometriai alak félperimetere.
4 képletű: R = (n - k) * TG (A / 2), ahol n - jelentése semiperimeter háromszög - annak egyik oldalán, és a TG (A / 2) - tangense fele ezen az oldalán a szemközti szög.
Az alábbi képlet segít megtalálni a kör sugarait, amely egy egyenlő oldalú háromszögbe van írva.
5. képlet: R = A * √3 / 6.
A kör sugara, amely egy jobb háromszögben szerepel
Ha a probléma a lábak hosszát adja, valamint a hipotenuzát, akkor a beírt kör sugarát az alábbiak szerint ismerjük fel.
1. képlet: R = (A + B-C) / 2, ahol A, B - a lábak, C - a hypotenuse.
Abban az esetben, ha csak két lábad van megadva, itt az ideje, hogy emlékezzen a pitagorai tételre, hogy a hipoténszujek megtalálhassák és felhasználhassák a fenti képletet.
C = √ (A² + B²).
A kör sugara, amely a térbe van írva
A négyzetbe írt kör négy pontot pontosan felosztja az érintés pontjaiban.
Formula 1: R = A / 2, ahol A - a négyzet oldalának hossza.
2. képlet: R = S / (P / 2), ahol S és P a tér területe és kerülete.