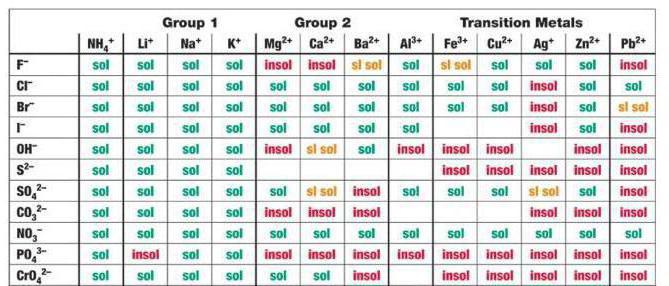
Alap MKT egyenlet és hőmérsékletmérés

A statisztikában előforduló folyamatok tanulmányozásarendszereket bonyolítja a részecskék minimális mérete és hatalmas számuk. Gyakorlatilag lehetetlen minden egyes részecskét külön figyelembe venni, ezért statisztikai értékeket vezetnek be: a részecskék átlagos sebességét, koncentrációjukat, a részecske tömegét. A rendszer állapotát jellemző mikroszkopikus paraméterekkel rendelkező képletet a gázok molekuláris kinetikus elméletének (MKT) alapegyenletének nevezik.

Egy kicsit a részecskék átlagos sebességéről

Először a részecskék mozgási sebességének meghatározása voltkísérletileg. Ismert a tananyag kísérletet Otto Stern, hozhatnak létre egy képet a részecskesebességeket. A kísérlet vizsgált a mozgás a ezüst atomok forgó hengerek: első helyhez kötött telepítés, majd amikor ez forog egy bizonyos szögsebességgel.

Ennek eredményeként azt találták, hogy a sebesség a molekulákezüst meghaladja a hangsebességet és 500 m / s. Az a tény nagyon érdekes, mert nehéz érzékelni a részecskék mozgásának ilyen sebességét az anyagokban.

Tökéletes gáz

A kutatás folytatása lehetségesCsak olyan rendszerben, amelynek paramétereit fizikai eszközökkel végzett közvetlen mérésekkel lehet meghatározni. A sebességet sebességmérővel mérik, de az a gondolat, hogy a sebességmérőt egy adott részecskehez csatlakoztatják, abszurd. A részecskék mozgásával kapcsolatos makroszkopikus paraméterek közvetlenül mérhetők.

Tekintsük a gáznyomást. A tartály falaira gyakorolt ​​nyomást úgy alakítják ki, hogy a gáz molekuláit az edénybe fújják. Az anyag gáznemű állapotának sajátossága a részecskék és a kis kölcsönhatás között elég nagy távolságra van. Ez lehetővé teszi a nyomás közvetlen mérését.

A kölcsönható testek bármely rendszerejellemzi a mozgás potenciális energiáját és kinetikus energiáját. A valódi gáz összetett rendszer. A potenciális energia változékonyságát nem lehet szisztematizálni. A probléma megoldható egy olyan modell bemutatásával, amely a gáz jellemző tulajdonságait hordozza, amely elhomályosítja az interakció komplexitását.

Az ideális gáz az anyagi állapot, amelybena részecskék kölcsönhatása elhanyagolható, az interakció potenciális energiája nulla. Jelentősnek tekinthető csak a mozgás energiája, amely a részecskék sebességétől függ.

Az ideális gáznyomás

Határozza meg a gáznyomás és a sebesség közötti összefüggésta részecskék mozgása lehetővé teszi az ideális gáz MKT alapegyenletét. A hajóban mozgó részecskék, amikor egy falhoz ütköznek, impulzust adnak neki, amelynek nagyságát Newton második törvénye alapján lehet meghatározni:

• FΔt = 2m₀v_x

A részecske lendületének változása rugalmas ütemben a sebesség horizontális összetevőjének változásával függ össze. F a részecskék oldalán a falon rövid ideig t hatást kifejtő erő; m₀ A részecske tömege.

Egy S felületen egy ideig Δt minden olyan gázrészecskék, amelyek a felszín irányában mozgó sebességgel ütköznek_x és Sv. térfogatú hengerben helyezkedik el_xAt. A részecskekoncentrációnál n a molekulák pontosan fele elmozdul a falhoz, a második felét - ellentétes irányban.

Miután figyelembe vettük az összes részecske ütközését, Newton törvényét írhatjuk a padra ható erőre:

• FΔt = nm₀v_x²SΔt

Mivel a gáznyomás a felületre merőleges erőnek az utóbbi területéhez viszonyított aránya, a következőket írhatjuk:

• p = F: S = nm₀v_x²

Az így létrejövő reláció, mint az alapvető MKT egyenlet, nem írhatja le az egész rendszert, mivel csak egy irányú mozgást veszünk figyelembe.

Maxwell eloszlás

Folyamatos gyakori ütközések gázrészecskékkel aa falak és egymás között a részecskék bizonyos statisztikai eloszlásának létrehozása a sebességek (energiák) szempontjából. Az összes sebességvektor iránya ugyanilyen valószínû. Ezt az eloszlást Maxwell-eloszlásnak nevezték el. 1860-ban ezt a mintát Maxwell alapította az MKT alapján. A terjesztési törvény legfontosabb paraméterei a sebesség: valószínű, a görbe maximális értékének felel meg, és az rms v_szögletes = √ <v²> A részecske sebességének átlagos négyszöge.

A gázhőmérséklet növekedése megegyezik a sebesség értékének növekedésével.

Azon tényből kiindulva, hogy minden sebesség azonos, és moduljaiknak azonos értéke van, feltételezzük, hogy:

• <v²> = <V_x²> + <V_y²> + <V_Z²>, Ahonnan: <v_x²> = <V²>: 3

Az alapvető MKT egyenlet figyelembe véve a gáznyomás átlagos értékét:

• p = nm₀<v²>: 3.

Ez a kapcsolat egyedülálló abban, hogy ez határozza meg a kapcsolat a mikroszkopikus paraméterek: sebesség, részecske tömege, szemcsék sűrűsége és a gáz nyomása, mint egy egész.

A részecskék kinetikus energiájának fogalmával az alap-MKT egyenletet másképp lehet újraírni:

• p = 2 nm₀<v²>: 6 = 2n <E_hogy>: 3

A gáznyomás arányos a részecskék kinetikus energiájának átlagértékével.

hőmérséklet

Érdekes, hogy a változatlan mennyiségű földgázbanZárt tartály kapcsolható össze a gáz nyomásával és az átlagos részecske energiával. A nyomás mérése a részecskék energiájának mérésével történhet.

Mit tegyek? Milyen értéket lehet összehasonlítani a kinetikus energiával? Ilyen érték a hőmérséklet.

A hőmérséklet az anyagok hõállapotának mértéke. A maga alkalmazott mérési hőmérővel, ak- amelyek azt a hőtágulása a munkaközeg (alkohol, higany) melegítés közben. A hőmérő skála kísérleti jelleggel jön létre. Általában ez adja címkék megfelelő pozícióban a munkaközeget egy bizonyos fizikai folyamatok során fellépő termikus változatlan állapotban (forrásban lévő vízzel, olvadó jég). A különböző hőmérők különböző méretűek. Például a skála Celsius, Fahrenheit.

Univerzális hőmérsékleti skála

Érdekesebb a függetlenség szempontjábóla munkaközeg tulajdonságai gázhőmérőként tekinthetők. A méretük nem függ a használt gáz típusától. Egy ilyen eszközben hipotetikusan azonosítani lehet azt a hőmérsékletet, amelyen a gáznyomás nullára fordul. A számítások azt mutatják, hogy ez az érték -273,15-nek felel meg ^{körülbelül}S. A hőmérsékleti skála (abszolút hőmérsékleti skála vagy Kelvin skála) 1848-ban került bevezetésre. Ennek a mérlegnek a fő pontja a nulla gáznyomás lehetséges hőmérséklete volt. Az egység skála szegmens egyenlő a Celsius skála egységértékével. A gázfolyamatok tanulmányozása során sokkal kényelmesebb az alapvető MKT egyenlet leírása a hőmérséklet alkalmazásával.

Nyomás és hőmérséklet viszony

Kísérletileg meg lehet győződni a gáznyomás arányosságáról a hőmérsékletére. Ugyanakkor megállapítást nyert, hogy a nyomás egyenesen arányos a részecske-koncentrációval:

• P = nkT,

ahol T az abszolút hőmérséklet, k állandó értéke 1,38 • 10^-23J / K.

Az alapérték, amely állandó értéket jelent minden gáz számára, a Boltzmann konstansnak nevezzük.

Összehasonlítva a nyomás függését a hőmérséklet és az MKT gázok alapvető egyenleteivel, írhatunk:

• <E_hogy> = 3kT: 2

A gázmolekulák mozgásának kinetikus energiájának átlagos értéke arányos a hőmérsékletével. Vagyis a hőmérséklet a részecske mozgásának kinetikus energiájának mértéke lehet.