A Maclaurin sorozat és bizonyos funkciók bomlása

Meg kell ismerni a magasabb matematikát,hogy az adott sorozat konvergencia-tartományához tartozó teljesítménysorozat összege egy differenciáló függvény, amely folyamatos és végtelenül sokszor eltérő. Felmerül a kérdés: lehet-e azt állítani, hogy egy adott önkényes függvény f (x) a teljesítménysorozat összege? Vagyis milyen körülmények között lehet az f-f feszültséget (x) teljesítménysorozattal ábrázolni? Az ilyen kérdés fontossága az, hogy az f (x) értéket a teljesítménysorozat több első mondatának, vagyis egy polinomnak az összegével helyettesítjük. A függvénynek egy meglehetősen egyszerű kifejezéssel - egy polinommal való - ilyen helyettesítése kényelmes megoldást nyújt a matematikai analízis egyes problémáinak megoldásában, nevezetesen: az integrálok megoldásában, a differenciálegyenletek számításában és így tovább.

Bizonyítottam, hogy egy olyan f (x) függvényre, ahol az (n + 1) -derrendű (az utolsó) - R; x₀ + R) egy bizonyos pont x = α, a következő képlet érvényes:

Ez a képlet viseli a híres tudós, Brooke Taylor nevét. Az előzőtől kapott sorozat neve a Maclaurin sorozat:

Egy olyan szabály, amely lehetővé teszi a Maclaurin sorozatba való bomlást:

1. Határozza meg az első, második, harmadik ... rendelések származékait.
2. Számítsd ki, hogy az x = 0-ban lévő származékok mennyiben egyenlők.
3. Jegyezze fel a Maclaurin sorozatot egy adott függvényre, majd határozza meg a konvergenciájának intervallumát.
4. Határozza meg az intervallumot (-R; R), ahol a maradék Maclaurin képlet

R_n(x) -> 0 mint n -> végtelen. Abban az esetben, ha létezik, a f (x) függvénynek meg kell egyeznie a Maclaurin sorozat összegével.

Most a Maclaurin sorozatot vesszük figyelembe az egyes funkciókhoz.

1. Így az első f (x) = e^x. Természetesen, a szingularitás szempontjából, egy ilyen funkció nagyon különböző rendelések származékai, és f^(K)(x) = e^x, ahol k egyenlő minden természetes számmal. Az x = 0 helyettesítjük. Elérjük f^(K)(0) = e⁰= 1, k = 1,2 ... A fentiekből kiindulva az e^x így fog kinézni:

2. A (z) f (x) = sin x függvényhez tartozó Maclaurin sorozat. Azonnal tisztázzuk, hogy a φ-th minden ismeretlen számára származtatott származékokat tartalmaz, továbbá f^"(x) = cos x = sin (x + n / 2), f^„”(x) = -sin x = sin (x + 2 * n / 2) ..., f^(K)(X) = sin (x + k * n / 2), ahol k egyenlő bármely pozitív egész szám. Ez azt jelenti, hogy egyszerű számítások, arra lehet következtetni, hogy a sorozat f (x) = sin x lesz, mint ez:

3. Most próbáljuk megfontolni a f (x) = cos x függvényt. Vannak tetszőleges sorrendjei az összes ismeretlen számára, és | f^(K)(x) | = cos (x + k * n / 2) | <= 1, k = 1,2 ... Ismét, bizonyos számítások elvégzésével megkapjuk, hogy az f (x) = cos x sorozata így fog kinézni:

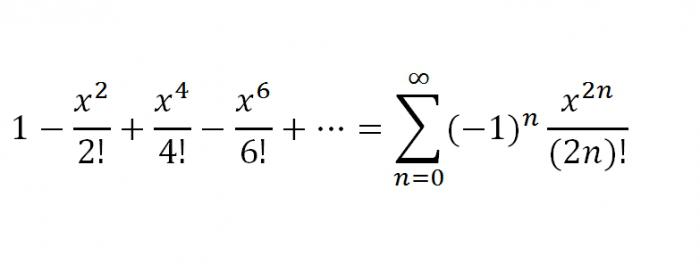
Tehát felsoroltuk azokat a legfontosabb funkciókat, amelyeklehet bontani egy Maclaurin sorozat, de kiegészíti Taylor sorozat néhány funkciót. Most felsoroljuk őket. Érdemes megjegyezni, hogy a Taylor és a Maclaurin sorozat fontos része a matematika sorozatának megoldására szolgáló workshopnak. Tehát a Taylor-sorozat.

1. Az első az f (x) = ln (1 + x) függvény sorozata. Az előző példákhoz hasonlóan, egy adott f (x) = ln (1 + x) esetén sorozatot adhatunk a Maclaurin sorozat általános alakja segítségével. Azonban ehhez a funkcióhoz a Maclaurin sorozat sokkal egyszerűbb. Egyes geometriai sorozatok integrálására egy ilyen minta f (x) = ln (1 + x) sorozatot kapunk:

2. És a második, amely végleges lesz a mi papíron, lesz egy sorozat f (x) = arctg x. A [-1; 1] intervallumhoz tartozó X esetén a kiterjesztés érvényes:

Ez minden. Ebben a cikkben a Taylor és a Maclaurin legelterjedtebb sorozatát a magasabb matematikában, különösen a gazdasági és műszaki egyetemeken vették figyelembe.